大家好,又见面了,我是你们的朋友全栈君。如果您正在找激活码,请点击查看最新教程,关注关注公众号 “全栈程序员社区” 获取激活教程,可能之前旧版本教程已经失效.最新Idea2022.1教程亲测有效,一键激活。
Jetbrains全家桶1年46,售后保障稳定
什么是hanoi塔?
汉诺塔问题:古代有一个梵塔,塔内有三个座A、B、C,A座上有64个盘子,盘子大小不等,大的在下,小的在上。有一个和尚想把这64个盘子从A座移到B座,但每次只能允许移动一个盘子,并且在移动过程中,3个座上的盘子始终保持大盘在下,小盘在上。如下图

问题解答
问题定义
我们把左边的柱子叫做A,中间的柱子叫做B,右边的柱子叫做C
hanoi`塔的搬运过程;
i :左边的柱子只有两个圆盘
ii:左边的柱子上面有三个圆盘 过程如下图: `在这种情况下,我们可以把上面的两个圆盘看作是一个,然后又回到了i情况,下图展示了三个圆盘的转移过程` 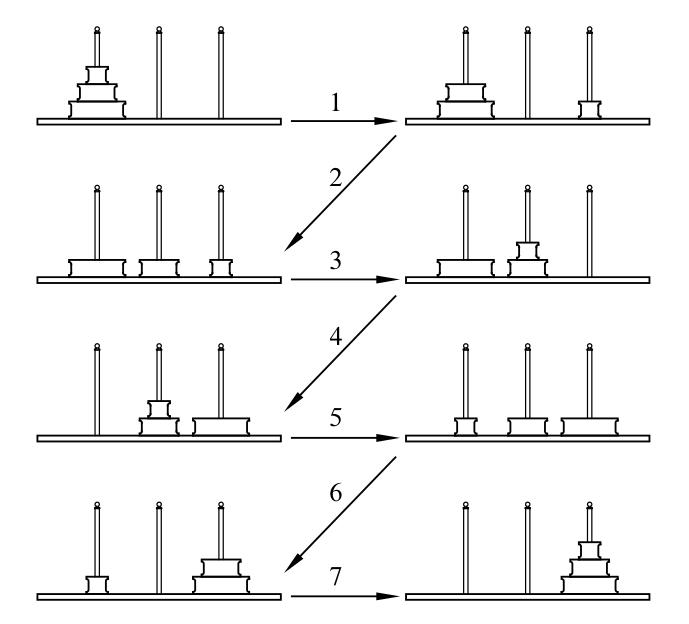 iii:左边的柱子上有四个圆盘的时候 在这种情况我们通过作图做出hanoi的转移流程是很困难的了,我们可以用在`ii`中提及到的过程,就是我们先把上面的三个看作是一个,我们第一步的目的就是把前三个移动到中间的柱子上去。下面简单说一下转移步骤 1. 将A柱子上面的三个移动到B柱子上面(借助C柱子) 2. 将A柱子上面中最下面的圆盘移动到C柱子上面 3. 将B柱子上面的所有圆盘移动到C柱子上面(借助A柱子) 过程如下图: 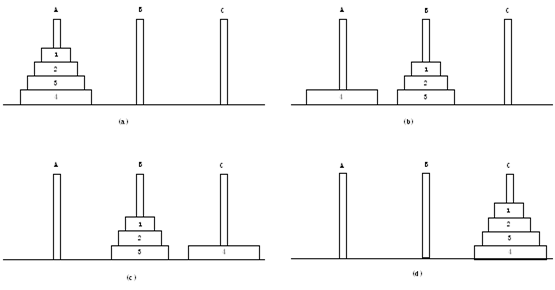 > 问题总结 > 通过上面的描述我们把hanoi移动的步骤一般化 >
- 将左边柱子上的
N-1个圆盘移动带中间的柱子上 - 将第N个圆盘移动到最右边的柱子
- 将中间柱子上的所有圆盘移动到最右边的柱子
下面我们给出具体的代码
void hanoi(int n,char A,char B,char C)
{
if(n<=1) {
printf("1 move %c to %c\n",A,C);
return ;
}
hanoi(n-1,A,C,B);
printf("%d move %c to %c \n",n,A,C);
hanoi(n-1,B,A,C);
}
不要在看了,这就是全部代码了。已经没有了
╭︿︿︿╮
{/ o o /}
( (oo) )
︶ ︶︶
以上是对hanoi塔的总体概述,下面就要聊一聊真正的代码流程!
代码详解
hanoi(n,A,B,C)代表的意义就是讲n个圆盘从A移动到C借助B;
- 当
n等于1的时候,就代表把当前A中最大的圆盘直接从A移动到C - 当
n等于2的时候,就调用hanoi(2,A,B,C)也就是执行下面的三个步骤下面就是本文中重点了
- 调用
honoi(1,A,C,B)就是相当于把***B柱和C柱交换***了 - 执行打印语句,不进行继续调用。所以不用交换柱子
- 调用
hanoi(1,B,A,C)相当于把***B柱和A柱交换***了
上面的语句可以表述为:
hanoi(1,A,C,B);
printf("%d move %c to %c \n",n,A,C);
hanoi(1,B,A,C);
这就是对代码的解释!
当圆盘更多的时候无非就是进行递归知道递归到上面的状态,比如有三个圆盘的时候,调用的是:
hanoi(2,A,C,B); //step1
printf("%d move %c to %c \n",n,A,C);
hanoi(2,B,A,C);
只要理解了前两个对后面的理解也就不难了!还有一点题外话,当递归到程序注释的step1的时候,会为后续语句分配空间但不执行!
hanoi塔还有一个进阶的题目就是判断当前的状态时第几个最优的状态,将在下篇文章进行讲述!
如果对我的文章感兴趣可以关注的公众号:云影原生。

发布者:全栈程序员-站长,转载请注明出处:https://javaforall.net/210738.html原文链接:https://javaforall.net



